
「さしがね」を知っていますか?
さしがねとは、大工さんが使う工具の一種。
表裏・内側・外側に目盛が付いているL字型の定規です。
材木などの長さを測ったり、線を引いたり、直角を確かめるときなどに使います。

シンプルな見た目とは裏腹に、たくさんのすごいところがあります。
なんと、さしがねのことを知るだけで、三角関数の「さいんこさいんたんじぇんと」が理解できるようになるんです!
昔から職人さんたちに愛されてきた理由がそこにあります。
計算のサポート
さしがねの目盛りは、ただ長さを測るためのものというだけではありません。
◆勾配の計算:屋根の傾斜など、勾配を出すための計算をサポートします。
◆角度の算出:特殊な目盛りを使って、様々な角度を算出できます。
二等辺三角形や直角三角形の比率が刻印されているものもあり、複雑な計算もスムーズにこなせます。
多様な使い方
測定や直角の確認以外にも、アイディア次第で使い方が広がります。
◆コンパスの代わりに:釘と鉛筆を使えば、大きな円を描くことも可能です。
◆水準器の補助:水準器と組み合わせることで、より正確な水平・垂直を出せます。
まさに「L字型の万能ツール」と言えるでしょう。
45° をさしがねで作る最も簡単な方法
▼やり方
1. 本尺(L字の長い方)と枝尺(L字の短い方)の 10と10 を材料端に合わせる。
2. できた線を結ぶ。
3. 1:1 なので 、これで45° 完成!
▼ 図(イメージ)

実はこれが「大工数学の核心」+「三角関数」!
さしがねは“サイン・コサイン・タンジェントを アナログで即座に再現できる道具”なのです。
さいんこさいんたんじぇんとってなんだっけ?
さいんこさいんたんじぇんと=「三角関数」を使うと、主に直角三角形について「角度」と「辺の長さ」の比率を求めることができます。
大工さんはさしがねを使って、この比率を元に、もう一方の材木の長さを算出したりしています。
ここからはサイン・コサイン・タンジェントについてそれぞれ大工さんの作業が数学とどう結びついているかを解説していきます。
が…さいんこさいんたんじぇんとアレルギーの方は、最後のまとめのひとことだけでも見て行ってください(笑)
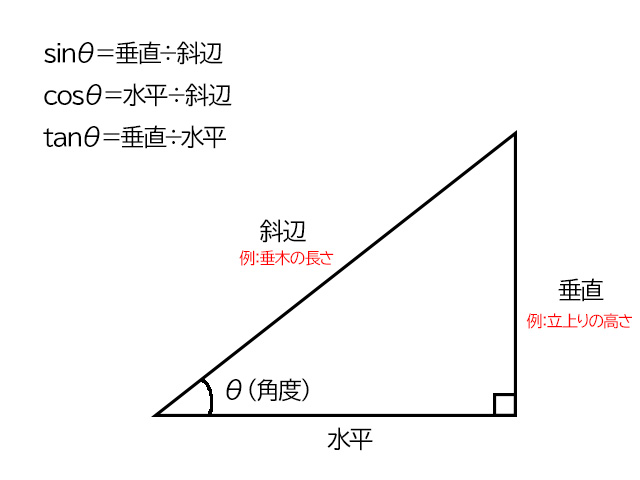
サイン(sin)× さしがね
sinθ=垂直 ÷ 斜辺
さしがねを使って斜めに線を引く=「斜辺」を作っていることになります。
大工さんが
◆材料の端に角度当てる
◆斜めに切る
この作業は、数学的なsinθ=垂直÷斜辺を自然に使っている状態なのです。
例えば一般的な日本家屋によく用いられる4寸勾配(tan 0.4、角度にして約21.8°)だと、sinθ (斜め材の長さに対する垂直の割合)=0.371
つまり、勾配材の「実際の長さ」や「垂木の長さ」を求める時に sin が使われていることになります。

コサイン(cos)× さしがね
cosθ=水平÷斜辺
勾配のある屋根の“実寸”を取るとき、大工さんは垂木の長さや梁の角度計算でcosθ を自然に使います。
先ほどの4寸勾配より少し角度のある5寸勾配(tanθ = 0.5、角度にして約26.5°)を例にとると
cosθ=0.894なので、斜辺(垂木の長さ)=水平長さ÷0.894で算出できることになります。
つまり、さしがねで角度を作る → 実寸を当てる → 材料を切るという作業は、完全にcosθの世界なのです。
タンジェント(tan)× さしがね
タンジェント(tan)=垂直(立上り)÷水平
大工さんが使う“●寸勾配”という屋根の角度の表し方は、tanθのお話。
先ほども登場した4寸勾配では、さしがねの水平10となります。
tanθ=立上り●÷さしがねの水平10
屋根が4寸勾配ということは、さしがねの水平10に対して垂直に4上がるという意味。
数学的な表し方ではtanθ=4/10=0.4となります。
つまり、さしがねで4寸勾配を取るということが、tanθの角度をアナログで作っているということになるのです。
まとめ:大工さんは「三角関数を体で使っている」!!
大工さんが使う言葉をさいんこさいんたんじぇんと=三角関数で表すと次のようになります。
4寸勾配はtanθ=0.4
5寸勾配はtanθ=0.5
垂木の長さ=水平長さ÷cosθ
垂木の上がり(高さ)=斜辺×sinθ
さしがねの10‐●合わせ=tanθの再現
まさに、さしがね=アナログ三角関数器具といえるのです!








